Page 36 - 教师纵横2020.1

教育观察 •教师纵横 互联网杂志
• •
教师纵横 互联网杂志

要有二次函数与线段、面积、相似三角形、角度、 利用【度量】量出 PD 的长和点 P 的横坐标 ，然
等腰三角形、直角三角形、特殊四边形相结合题型。 后利用【绘图】绘制点（ ），最后点击因
图形繁杂是学生解题的障碍，数形结合的思想是学 为点 P 和结果点（ ）利用【构造】中的轨
生难以逾越的鸿沟。通过几何画板的绘图，度量， 迹得出如图 2 所示的图形。从图中不难看出 的轨

构造内部、轨迹、垂线、平行线，数据计算和变换 迹是一条抛物线，最大值就是顶点的纵坐标的值，
功能绘制出图形就能轻松地找到解题思路。如 2019 通过这样的操作轻易地突破难点一。再来看看难点

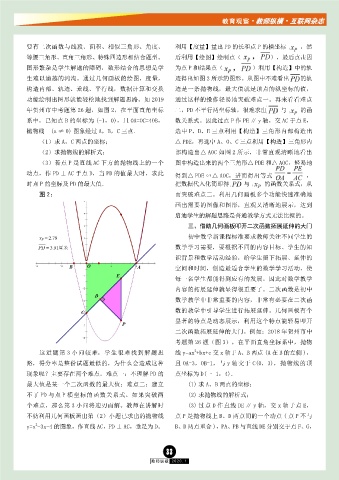
年贺州市中考题第 26 题，如图 2，在平面直角坐标 二，PD 不平行两坐标轴，很难求出 与 的函
系中，已知点 B 的坐标为 (-1，0)，且 OA=OC=4OB， 数关系式。因此过点 P 作 PE ∥ y 轴，交 AC 于点 E，
抛物线 (a ≠ 0) 图象经过 A，B，C 三点． 选中 P、D、E 三点利用【构造】三角形内部构造出
（1）求 A，C 两点的坐标； △ PDE，再选中 A、O、C 三点利用【构造】三角形内

（2）求抛物线的解析式； 部构造出△ AOC 如图 2 所示，非常直观清晰地看出
（3）若点 P 是直线 AC 下方的抛物线上的一个 图中构造出来的两个三角形△ PDE 和△ AOC，轻易地
动点，作 PD ⊥ AC 于点 D，当 PD 的值最大时，求此 得到△ PDE ∽△ AOC，进而得出等式 ，

时点 P 的坐标及 PD 的最大值． 把数据代入化简即得 与 的函数关系式，从
图 2： 而突破难点二。利用几何画板多个功能快速准确地
画出需要的图像和图形，直观又清晰地展示，达到

启迪学生的解题思路是普通教学方式无法比拟的。
三、借助几何画板叩开二次函数拓展延伸的大门
初中数学新课程标准要求教师关注不同学生的

数学学习需要，要根据不同的内容目标、学生的知
识背景和数学活动经验，给学生留下拓展、延伸的
空间和时间，创造最适合学生的数学学习活动，使
每一名学生都能得到应有的发展。因此对数学教学

内容的拓展延伸就显得很重要了。二次函数是初中
数学教学中非常重要的内容，非常有必要在二次函
数的教学中引导学生进行拓展延伸。几何画板有个

显著的特点是动态展示，利用这个特点能轻易叩开
二次函数拓展延伸的大门。例如：2018 年贺州市中
考题第 26 题（图 3），在平面直角坐标系中，抛物
2
这道题第 3 小问较难，学生很难找到解题思 线 y=ax +bx+c 交 x 轴于 A、B 两点 (A 在 B 的左侧 )，
路，得分率是整份试题最低的，为什么会造成这种 且 OA=3，OB=1，与 y 轴交于 C(0，3)，抛物线的顶
现象呢？主要存在两个难点。难点一：不理解 PD 的 点坐标为 D( ﹣ 1，4)．

最大值是某一个二次函数的最大值；难点二：建立 (1) 求 A、B 两点的坐标；
不了 PD 与点 P 横坐标的函数关系式。如果突破两 (2) 求抛物线的解析式；
个难点，那么第 3 小问将迎刃而解。教师在讲解时 (3)过点D作直线DE∥y轴，交x轴于点E，
不妨利用几何画板画出第（2）小题已求出的抛物线 点 P 是抛物线上 B、D 两点间的一个动点 ( 点 P 不与

2
y=x -3x-4 的图象，作直线 AC，PD ⊥ AC，垂足为 D。 B、D 两点重合 )，PA、PB 与直线 DE 分别交于点 F、G，

33

教师纵横 2020.1